4.2.0我的笔记代码都可以正常渲染,我换行用了\来控制行距;
4.2.1我的笔记代码带有\的全部渲染失败,能否回退软件版本?
我急着使用 没时间等你们mn4团队修好所有bug更新4.2.2
带有\ \ [ 2pt]类似格式
Hello
源码使用三个`包裹发送下
Kind Regards,
Support Team
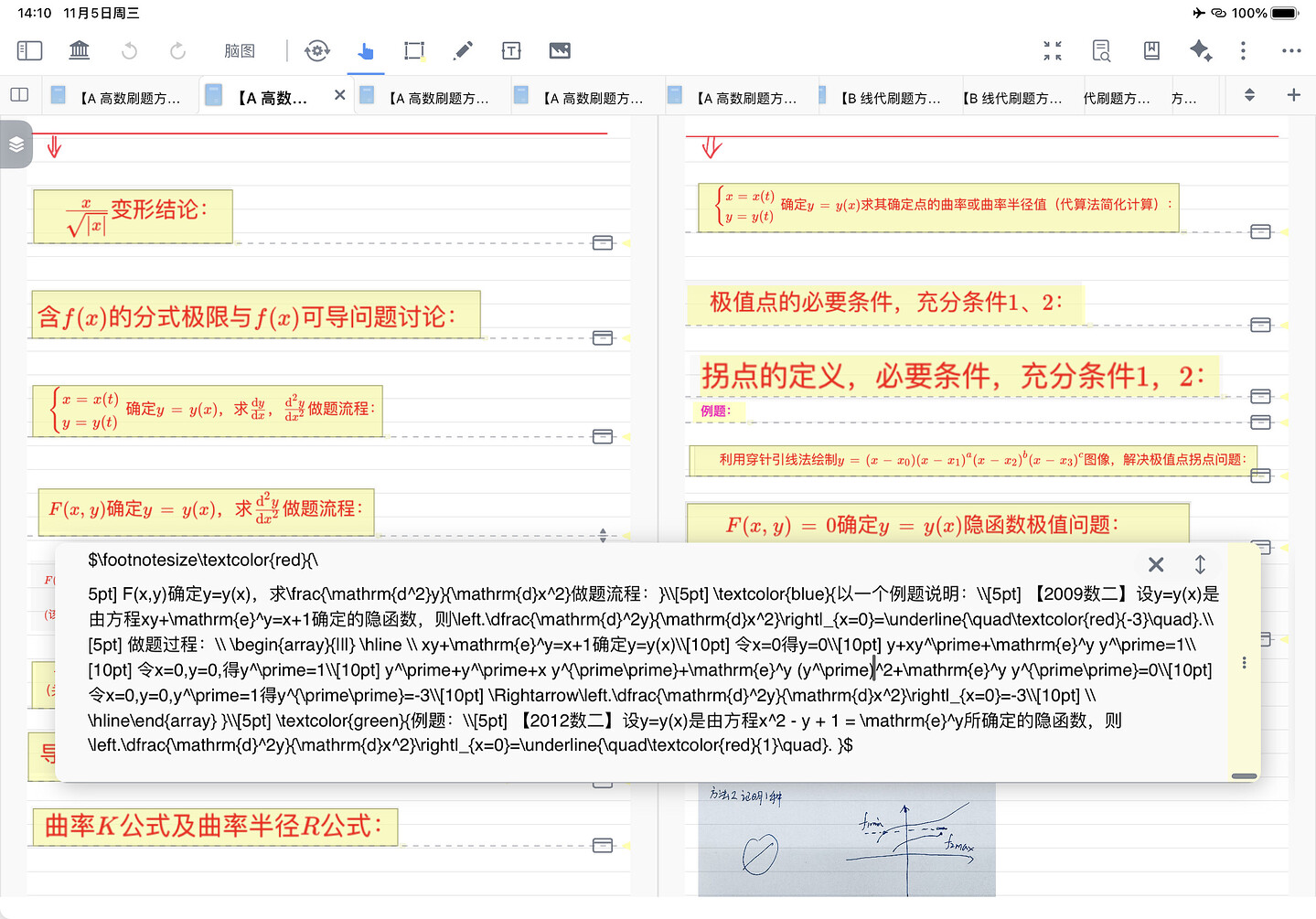
F(x,y)确定y=y(x),求\frac{\mathrm{d^2}y}{\mathrm{d}x^2}做题流程:}\\[5pt]
\textcolor{blue}{以一个例题说明:\\[5pt]
【2009数二】设y=y(x)是由方程xy+\mathrm{e}^y=x+1确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=\underline{\quad\textcolor{red}{-3}\quad}.\\[5pt]
做题过程:\\
\begin{array}{|l|}
\hline
\\
xy+\mathrm{e}^y=x+1确定y=y(x)\\[10pt]
令x=0得y=0\\[10pt]
y+xy^\prime+\mathrm{e}^y y^\prime=1\\[10pt]
令x=0,y=0,得y^\prime=1\\[10pt]
y^\prime+y^\prime+x y^{\prime\prime}+\mathrm{e}^y (y^\prime)^2+\mathrm{e}^y y^{\prime\prime}=0\\[10pt]
令x=0,y=0,y^\prime=1得y^{\prime\prime}=-3\\[10pt]
\Rightarrow\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=-3\\[10pt]
\\
\hline\end{array}
}\\[5pt]
\textcolor{green}{例题:\\[5pt]
【2012数二】设y=y(x)是由方程x^2 - y + 1 = \mathrm{e}^y所确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=\underline{\quad\textcolor{red}{1}\quad}.
}$```之前这些代码都是可以正常渲染出来的,我今天上午更新了4.2.1之后,包含$\\[5pt]$这样的latex代码都渲染不出来了,目前我初步断定是新版本的问题,因为我上午还在编写latex代码,还能正常使用手动换行指定间距指令,上午更新完中午吃完饭下午再编写就发现渲染出了问题。
Hello
第一句代码是不是不太对,但是其他都是可以渲染的,最后一个$删掉就可以渲染下边的部分
Kind Regards,
Support Team
我在4.2.0版本中,这些代码都是可以正常渲染出来。
但是我在4.2.1版本中,这些代码全部都渲染不出来了。
我这个代码前面是首尾一个$包裹住的,里面用的是latex代码语法,用的都是Markdown轻量编辑器可以识别的,在你回复的内容中,说源码前面有问题,我看了一下,符合latex语法。
最后,我不想纠结版本哪里出现了bug导致无法渲染的问题,能否回退4.2.0?
源码是这样的,我不清楚你说的用```包裹是不是首尾包裹的意思,这里,是我未经修改的源码:
$\footnotesize\textcolor{red}{\[5pt]
F(x,y)确定y=y(x),求\frac{\mathrm{d^2}y}{\mathrm{d}x^2}做题流程:}\[5pt]
\textcolor{blue}{以一个例题说明:\[5pt]
【2009数二】设y=y(x)是由方程xy+\mathrm{e}^y=x+1确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|{x=0}=\underline{\quad\textcolor{red}{-3}\quad}.\[5pt]
做题过程:\
\begin{array}{|l|}
\hline
\
xy+\mathrm{e}^y=x+1确定y=y(x)\[10pt]
令x=0得y=0\[10pt]
y+xy^\prime+\mathrm{e}^y y^\prime=1\[10pt]
令x=0,y=0,得y^\prime=1\[10pt]
y^\prime+y^\prime+x y^{\prime\prime}+\mathrm{e}^y (y^\prime)^2+\mathrm{e}^y y^{\prime\prime}=0\[10pt]
令x=0,y=0,y^\prime=1得y^{\prime\prime}=-3\[10pt]
\Rightarrow\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|{x=0}=-3\[10pt]
\
\hline\end{array}
}\[5pt]
\textcolor{green}{例题:\[5pt]
【2012数二】设y=y(x)是由方程x^2 - y + 1 = \mathrm{e}^y所确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=\underline{\quad\textcolor{red}{1}\quad}.
}$
$\footnotesize\textcolor{red}{\\[5pt]
F(x,y)确定y=y(x),求\frac{\mathrm{d^2}y}{\mathrm{d}x^2}做题流程:}\\[5pt]
\textcolor{blue}{以一个例题说明:\\[5pt]
【2009数二】设y=y(x)是由方程xy+\mathrm{e}^y=x+1确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=\underline{\quad\textcolor{red}{-3}\quad}.\\[5pt]
做题过程:\\
\begin{array}{|l|}
\hline
\\
xy+\mathrm{e}^y=x+1确定y=y(x)\\[10pt]
令x=0得y=0\\[10pt]
y+xy^\prime+\mathrm{e}^y y^\prime=1\\[10pt]
令x=0,y=0,得y^\prime=1\\[10pt]
y^\prime+y^\prime+x y^{\prime\prime}+\mathrm{e}^y (y^\prime)^2+\mathrm{e}^y y^{\prime\prime}=0\\[10pt]
令x=0,y=0,y^\prime=1得y^{\prime\prime}=-3\\[10pt]
\Rightarrow\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=-3\\[10pt]
\\
\hline\end{array}
}\\[5pt]
\textcolor{green}{例题:\\[5pt]
【2012数二】设y=y(x)是由方程x^2 - y + 1 = \mathrm{e}^y所确定的隐函数,则\left.\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}\right|_{x=0}=\underline{\quad\textcolor{red}{1}\quad}.
}$